[ 目次, 前節, 次節, 索引 ]

A 000        C 010        E 100        G 110
B 001        D 011        F 101        H 111

   ASCIIや上の AからH 符号のような符号は, 通信文中の各文字を同じビット数で表現するので 固定長(fixed-length)符号という. しかし時には異る記号は異るビット長で表現する 可変長(variable-length)符号を使う利点もある. 例えば モールス符号は, アルファベットの各文字に同数の短点と長点は使っていない. 特に一番よく出てくるEは1個の短点で表現する. 一般に通信文のある記号が頻繁に現れ, 別の記号が殆んど現れなければ, 頻繁な記号に短い符号を割り当てることでデータを更に効率よく(つまり通信文当りのビット数を減らして)符号化出来る. AからHの文字に対する次の符号を考えてみよう.

A 0           C 1010        E 1100        G 1110
B 100         D 1011        F 1101        H 1111

   可変長符号を使う時の問題点の一つは, 0と1の列を読みながら, 記号の終りに来たことをどう知るかにある. モールス符号はこの問題を各文字の短点と長点の列の後に特別な 分離符号(separator code) (この場合は休止)を置いて解決した. 別の解決法はある記号の符号全体が他の記号の符号の初め(語頭(prefix))にならないように符号を設計する. こういう符号は 語頭符号(prefix code)という. 上の例ではAは0, Bは100と符号化されるので, 他の記号は0や100で始る符号を持ち得ない.

   一般に通信文中の記号の相対頻度を符号化に利用した可変長語頭符号を使うと, かなり節約出来る. このやり方の一つは, 発見者 David Huffmanに従ってHuffman符号化法という. Huffman符号は葉のところに符号化する文字のある 二進木で表現する. 木の, 葉でない節には, その節の下にある葉の記号をすべて含む集合が付随している. 更に葉のところの各文字には重み(相対頻度)が割り当ててあり, 葉でない節にはその下の葉の重みを足し合せた重みが割り当てられている. 重みは符号化, 復号化の時には使わない. 次に木を構成するのに重みがどう役立つかを見よう.

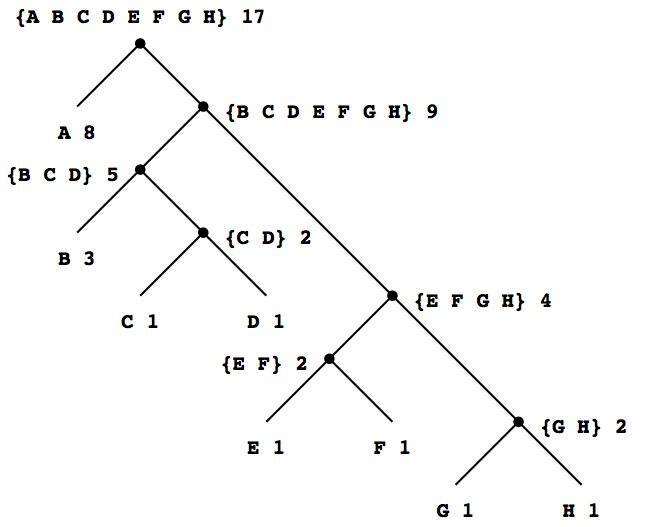
   図2.18は上のAからH符号に対するHuffman木を示す. 葉の重みはこの木が, Aが相対頻度8, Bが3で, 他が1の通信文向けに設計されたことを示している.



図2.18 Huffman符号化木

   Huffman木があれば, ルートから出発しその記号を持つ葉に到達するまで下っていくことで, ある文字の符号が見つかる. 左の枝へ下る度に符号に0を追加し, 右の枝へ下る度に1を追加する. (どちらの枝へ進むかは, どちらの枝にその記号の葉があるか, または集合にその記号を含んでいるかを見て決める.) 例えば図2.18のルートから出発し, Dの葉へは, 右の枝, 左の枝, 右の枝, 右の枝と進む; そこでDの符号は1011である.

   Huffman木を使ってビット列を復号化するには, ルートから始めビット列の0と1の並びを左の枝へ下るか右の枝へ下るか決めるのに使う. 葉に到達する度に, 通信文の新しい記号を作り出し, そこからルートへ戻って次の記号を探し始める. 例えば上の木と, 列10001010が与えられたとする. ルートから出発し, (先頭のビットは1なので)右へ下り, (二番目のビットは0なので)左へ下り, (三番目のビットも0なので)左へ下る. するとBの葉へ到達するから, 符号化通信文の最初の記号はBである. さてもう一度ルートから出発し, 列の次のビットが0だから左へ下る. Aの葉へ到達する. 更にまたルートから残りの列1010を持って出発し, 右, 左, 右, 左と進んでCへ到達する. つまり通信文はBACであった.

Huffman木の生成

   Huffman木の生成アルゴリズムは単純である. 最小頻度の記号をルートから最も遠くに置くという発想である. 符号を構成しようとする初期データから決る記号と頻度からなる葉の節の集合から始める. さて最小の重みを持つ二つの葉を見つけ, 合体させてこの節を左と右に持つ節を作る. 最初の集合からこの二つの節を除去し, 新しい節を置く. この手続きを繰り返す. 毎回最小重みの節を合体させ. 集合から除去し, これらの二つの節を左と右に持つ節で取り替える. 遂に節が一つになったら終了し, これが全体の木のルートになる. 以下が図2.18のHuffman木が生成される様子である:

最初の葉    {(A 8)  (B 3)  (C 1)  (D 1)  (E 1)  (F 1)  (G 1)  (H 1)}
合体        {(A 8)  (B 3)  ({C D} 2)  (E 1)  (F 1)  (G 1)  (H 1)}
合体        {(A 8)  (B 3)  ({C D} 2)  ({E F} 2)  (G 1)  (H 1)}
合体        {(A 8)  (B 3)  ({C D} 2)  ({E F} 2)  ({G H} 2)}
合体        {(A 8)  (B 3)  ({C D} 2)  ({E F G H} 4)}
合体        {(A 8)  ({B C D} 5)  ({E F G H} 4)}
合体        {(A 8)  ({B C D E F G H} 9)}
最後の合体  {({A B C D E F G H} 17)}

Huffman木の表現

   葉の節は記号leaf, その葉の記号と重みからなるリストで表現する:

(define (make-leaf symbol weight)
  (list 'leaf symbol weight))


(define (leaf? object)
  (eq? (car object) 'leaf))


(define (symbol-leaf x) (cadr x))


(define (weight-leaf x) (caddr x))

(define (make-code-tree left right)
  (list left
        right
        (append (symbols left) (symbols right))
        (+ (weight left) (weight right))))

(define (left-branch tree) (car tree))


(define (right-branch tree) (cadr tree))


(define (symbols tree)
  (if (leaf? tree)
      (list (symbol-leaf tree))
      (caddr tree)))


(define (weight tree)
  (if (leaf? tree)
      (weight-leaf tree)
      (cadddr tree)))

復号化手続き

(define (decode bits tree)
  (define (decode-1 bits current-branch)
    (if (null? bits)
        '()
        (let ((next-branch
               (choose-branch (car bits) current-branch)))
          (if (leaf? next-branch)
              (cons (symbol-leaf next-branch)
                    (decode-1 (cdr bits) tree))
              (decode-1 (cdr bits) next-branch)))))
  (decode-1 bits tree))

(define (choose-branch bit branch)
  (cond ((= bit 0) (left-branch branch))
        ((= bit 1) (right-branch branch))
        (else (error "bad bit -- CHOOSE-BRANCH" bit))))

重みつき要素の集合

   葉と木の集合を, 重みの大きくなる順に並べたリストの要素として表現する. 次の集合を構成するadjoin-set手続きは, 問題2.61に書いたものと似ている; しかし項は重みで比べられ, 集合に追加される要素は決して前から存在していることはない.

(define (adjoin-set x set)
  (cond ((null? set) (list x))
        ((< (weight x) (weight (car set))) (cons x set))
        (else (cons (car set)
                    (adjoin-set x (cdr set))))))

   次の手続きは((A 4) (B 2) (C 1) (D 1))のような記号と頻度の対のリストをとり, Huffmanアルゴリズムにより, 直ぐに合体される葉の, 最初の順序づけられた集合を構成する.

(define (make-leaf-set pairs)
  (if (null? pairs)
      '()
      (let ((pair (car pairs)))
        (adjoin-set (make-leaf (car pair)    ; 記号
                               (cadr pair))  ; 頻度
                    (make-leaf-set (cdr pairs))))))

(define sample-tree
  (make-code-tree (make-leaf 'A 4)
                  (make-code-tree
                   (make-leaf 'B 2)
                   (make-code-tree (make-leaf 'D 1)
                                   (make-leaf 'C 1)))))

(define sample-message '(0 1 1 0 0 1 0 1 0 1 1 1 0))

(define (encode message tree)
  (if (null? message)
      '()
      (append (encode-symbol (car message) tree)
              (encode (cdr message) tree))))

(define (generate-huffman-tree pairs)
  (successive-merge (make-leaf-set pairs)))

A     2          NA   16
BOOM  1          SHA   3
GET   2          YIP   9
JOB   2          WAH   1

42 Huffman符号の数学的性質についての議論は Hamming 1980参照

[ 目次, 前節, 次節, 索引 ]