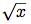 が関数y
が関数y  x/yの不動点であるという認識から始め, 新しい平方根手続きを不動点探索として書いた. 次いで近似を収束させるために,
平均緩和を使った. 平均緩和はそれ自身有用な一般的技法である. つまりある関数fに対し, xでの値がxとf(x)の平均である関数を考える.
x/yの不動点であるという認識から始め, 新しい平方根手続きを不動点探索として書いた. 次いで近似を収束させるために,
平均緩和を使った. 平均緩和はそれ自身有用な一般的技法である. つまりある関数fに対し, xでの値がxとf(x)の平均である関数を考える.
この考えを示すために, 1.3.3節の終りにあった不動点の例をもう一度見よう.
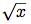 が関数y
が関数y  x/yの不動点であるという認識から始め, 新しい平方根手続きを不動点探索として書いた. 次いで近似を収束させるために,
平均緩和を使った. 平均緩和はそれ自身有用な一般的技法である. つまりある関数fに対し, xでの値がxとf(x)の平均である関数を考える.
x/yの不動点であるという認識から始め, 新しい平方根手続きを不動点探索として書いた. 次いで近似を収束させるために,
平均緩和を使った. 平均緩和はそれ自身有用な一般的技法である. つまりある関数fに対し, xでの値がxとf(x)の平均である関数を考える.
平均緩和の考え方を次の手続きで表す.
(define (average-damp f) (lambda (x) (average x (f x))))average-dampは引数として手続きfをとり, その値として(lambdaで作り出された)手続き, つまりある数xに作用させるとx と(f x)の平均を返す手続き, を返す手続きである. 例えば average-dampをsquareに作用させると, ある数値xに対して, xとx2の平均を値とするような手続きを作り出す. この返された手続きを10に作用させると10と100の平均, つまり55を返す:59
((average-damp square) 10) 55
average-dampを使うと平方根の手続きが次のように書ける:
(define (sqrt x)
(fixed-point (average-damp (lambda (y) (/ x y)))
1.0))
この形式化は三つの考え方: 不動点の探索, 平均緩和とy  x/yを使っていることに注意しよう. この平方根の形式化を1.1.7節にあった最初のものと比べるとためになる. この二つの手続きは同じプロセスを表すことを覚えておこう. またプロセスを抽象を使って表すと考え方が遥かに明瞭になることにも注意しよう. 一般にプロセスの手続きとしての形式化にはいろいろな方法がある. 経験あるプログラマは, 特に明快な手続きの形式化をどう選ぶか, またプロセスの有用な部分が他の応用にも再利用出来るようなまとまった存在として, どこに見えているかを知っている. 再利用の単純な例として, xの立方根が関数y
x/yを使っていることに注意しよう. この平方根の形式化を1.1.7節にあった最初のものと比べるとためになる. この二つの手続きは同じプロセスを表すことを覚えておこう. またプロセスを抽象を使って表すと考え方が遥かに明瞭になることにも注意しよう. 一般にプロセスの手続きとしての形式化にはいろいろな方法がある. 経験あるプログラマは, 特に明快な手続きの形式化をどう選ぶか, またプロセスの有用な部分が他の応用にも再利用出来るようなまとまった存在として, どこに見えているかを知っている. 再利用の単純な例として, xの立方根が関数y  x/y2の不動点であることに注意すれば, 平方根の手続きを立方根を得るものに直ちに一般化出来る:60
x/y2の不動点であることに注意すれば, 平方根の手続きを立方根を得るものに直ちに一般化出来る:60
(define (cube-root x)
(fixed-point (average-damp (lambda (y) (/ x (square y))))
1.0))
 g(x)が微分可能な関数であれば, 方程式g(x) = 0の解は
g(x)が微分可能な関数であれば, 方程式g(x) = 0の解は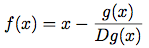
 f(x)の不動点である. Newton法は,
関数fの不動点を見つけることで解の近似値を求めるという, 上で見た不動点法の応用である.61
多くの関数gにとり, xの十分によい最初の予測値があれば, Newton法はg(x) =
0の解へ非常に速く収束する.62
f(x)の不動点である. Newton法は,
関数fの不動点を見つけることで解の近似値を求めるという, 上で見た不動点法の応用である.61
多くの関数gにとり, xの十分によい最初の予測値があれば, Newton法はg(x) =
0の解へ非常に速く収束する.62
Newton法を手続きとして実装するには, 微分を表さなければならない. 「微分」は平均緩和と同様に, 関数を関数に変換する何かである. 例えば関数x
 x3の微分は関数x
x3の微分は関数x  3x2である. 一般にgが関数でdx
が微小なら, gの微分Dgはxにおけるその値が(dxの微小な極限で)
3x2である. 一般にgが関数でdx
が微小なら, gの微分Dgはxにおけるその値が(dxの微小な極限で)
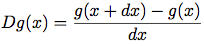
で与えられる関数である. そこで微分は(dxを例えば0.00001として)
(define dx 0.00001)と定義しておき, 手続き
(define (deriv g)
(lambda (x)
(/ (- (g (+ x dx)) (g x))
dx)))
と表せる.
average-dampと同様に, derivも引数として手続きをとり, 値として手続きを返す手続きである. 例えばx  x3の5での微分の近似値をとると(正確な値は75)
x3の5での微分の近似値をとると(正確な値は75)
(define (cube x) (* x x x)) ((deriv cube) 5) 75.00014999664018と評価出来る.
derivの助けがあれば, Newton法が不動点プロセスとして表せる.
(define (newton-transform g)
(lambda (x)
(- x (/ (g x) ((deriv g) x)))))
(define (newtons-method g guess)
(fixed-point (newton-transform g) guess))
newton-transformは本節の最初の式を表し, それを使えば
newtons-methodはすぐ定義出来る. それは引数として零点を見つけようとする関数を計算する手続きと, 最初の予測値をとる.
例えばxの平方根を見つけるのに,予測値を1から始めて, 関数y  y2 - xの零点を見つけるNewton法が使える.63
そこでまた別の平方根の手続きが出来る:
y2 - xの零点を見つけるNewton法が使える.63
そこでまた別の平方根の手続きが出来る:
(define (sqrt x)
(newtons-method (lambda (y) (- (square y) x))
1.0))
(define (fixed-point-of-transform g transform guess) (fixed-point (transform g) guess))この非常に一般的な手続きは引数としてある関数を計算する手続きg, gを変換する手続き, および最初の予測値をとり, 結果として変換された関数の不動点を返す.
この抽象を使うと, 本節の初めの第一の平方根計算(y  x/yを平方緩和した不動点)をこの一般的方法の特殊化として書き直せる:
x/yを平方緩和した不動点)をこの一般的方法の特殊化として書き直せる:
(define (sqrt x)
(fixed-point-of-transform (lambda (y) (/ x y))
average-damp
1.0))
同様に本節の第二の平方根計算(y  y2 - xのNewton変換の不動点を見つけるというNewton法の特殊化)も
y2 - xのNewton変換の不動点を見つけるというNewton法の特殊化)も
(define (sqrt x)
(fixed-point-of-transform (lambda (y) (- (square y) x))
newton-transform
1.0))
と表せる.
1.3節の初めの方で, 合成手続きは, それにより計算の一般的方法がプログラム言語の確かな要素として表せるが故に, 極めて重要な抽象機構であることを見た. また高階手続きがあると, 更なる抽象を作り出すためにこれらの一般的方法が操作出来るようになることも知った.
われわれはプログラマとして, プログラムの根底にある抽象を見つけ, より強力な抽象化が出来るよう, その上に構成し, 一般化するよう努めなければならない. これはプログラムを可能な限り抽象的に書くべしというのではない; 経験を積んだプログラマは, 自分の仕事に適した抽象のレベルを選ぶことを知っている. しかし抽象を使って考えることが出来るのは, 新しい状況になった時に, すぐ応用出来るため, 大切である. 高階手続きの重要さは, それにより抽象をプログラム言語の要素として確かに表せ, 他の計算要素のように扱えるという点にある.
一般にプログラム言語には, 計算要素を扱う方法にいろいろな制限があるものだ. 制限の殆んどない要素は
第一級(first-class)身分を持つという. 第一級要素の「権利と特権」は:64
• 変数として名前がつけられる.
• 手続きに引数として渡せる.
• 手続きの結果として返される.
• データ構造に組み込める.65
である. Lispは他の通常のプログラム言語と違い, 手続きに完全な第一級身分を授与した. そのため, 効率のよい実装は難しくなったが, 表現力として得たものは絶大である.66
問題 1.40
newtons-methodの手続きと一緒に
(newtons-method (cubic a b c) 1)の形の式で使い, 三次式x3 + ax2 + bx + cの零点を近似する手続き cubicを定義せよ.
(((double (double double)) inc) 5)はどういう値を返すか.
 f(g(x))と定義する. 合成関数を実装する手続きcomposeを定義せよ. 例えばincが引数に1を足す手続きとすれば
f(g(x))と定義する. 合成関数を実装する手続きcomposeを定義せよ. 例えばincが引数に1を足す手続きとすれば((compose square inc) 6) 49
 x + 1とすると, fのn回作用は関数x
x + 1とすると, fのn回作用は関数x  x + nである.
fが数を二乗する演算なら, fのn回作用は引数を2n乗する関数である.
入力としてfを計算する手続きと, 正の整数nをとり, fのn回作用を計算する手続きを書け. その手続きは:
x + nである.
fが数を二乗する演算なら, fのn回作用は引数を2n乗する関数である.
入力としてfを計算する手続きと, 正の整数nをとり, fのn回作用を計算する手続きを書け. その手続きは:
((repeated square 2) 5) 625のように使えなければならない. ヒント:問題1.42のcomposeを使うと便利である.
 x/yの不動点を素朴に見つけることで平方根を計算する試みは収束せず, 平均緩和が役立つことを見た. 同じ方法で, y
x/yの不動点を素朴に見つけることで平方根を計算する試みは収束せず, 平均緩和が役立つことを見た. 同じ方法で, y  x/y2の平均緩和の不動点として立方根を見つけることが出来る.
困ったことに, この方法は四乗根には使えない. 単一の平均緩和はy
x/y2の平均緩和の不動点として立方根を見つけることが出来る.
困ったことに, この方法は四乗根には使えない. 単一の平均緩和はy  x/y3の不動点を収束させるには十分でない. 一方二回平均緩和すると(つまりy
x/y3の不動点を収束させるには十分でない. 一方二回平均緩和すると(つまりy  x/y3の平均緩和の平均緩和を使うと)不動点探索は収束する. y
x/y3の平均緩和の平均緩和を使うと)不動点探索は収束する. y  x/yn-1の平均緩和を繰り返し使った不動点探索として
n乗根を計算するのに, 何回の平均緩和が必要か実験してみよ. この結果を利用し, fixed-point, average-dampおよび問題1.43の
repeatedを使い, n乗根を計算する単純な手続きを実装せよ. 必要な算術演算は基本手続きとして使えるとせよ.
x/yn-1の平均緩和を繰り返し使った不動点探索として
n乗根を計算するのに, 何回の平均緩和が必要か実験してみよ. この結果を利用し, fixed-point, average-dampおよび問題1.43の
repeatedを使い, n乗根を計算する単純な手続きを実装せよ. 必要な算術演算は基本手続きとして使えるとせよ.
59
この組合せは, その演算子自身が組合せであることに注意しよう.
こういう組合せが作れることは, 問題1.4で見たが, それはたわいない例であった. 今からそういう組合せが---高階手続きが値として返した手続きを作用させる時---本当に必要であることを見ていく.
60
更なる一般化は問題1.45
参照
61
微積分の入門書には通常Newton法をxn+1 = xn
- g(xn)/Dg(xn)の近似値の列を使う方法と書いてある. プロセスを扱う言語があり, 不動点の考え方を使えば, この方法の記述は単純になる.
62
Newton法がいつでも収束するとは限らないが,うまくいく場合には, 反復の度に近似値の解に対する精度の桁数が倍になることが示される.
そういう場合, Newton法は区間二分法よりずっと速く収束する.
63
平方根を見つける時は,
Newton法はどういう初期値から出発しても正しい解に急速に収束する.
64
プログラム言語要素の第一級身分という考えは英国の計算機科学者
Christopher Strachey(1916--1975)による.
65
この例は2章でデータ構造を紹介した後で見よう.
66
第一級手続きの実装の大きな代価は, 手続きを値として返すためには, 手続きを実行しない時でも, 自由変数のための記憶場所をとっておく必要があることだ. 4.1節で学ぶSchemeの実装では, これらの変数は手続きの環境の中に格納してある.